Compleja | Sea epsilon...

En el post anterior describimos a los elementos de $PSL(2,\mathbb{R})$ segun tres tipos. Modulo conjugación, estos elementos se caracterizan por, o bien fijar un punto en el plano hiperbólico, o bien fijar un elemento en la frontera (de modo atractor), o bien fijar dos elementos en la frontera (uno atractor y otro repulsor). Vimos que en particular, los elementos elípticos, luego de conjugarlos de una manera adecuada, son de la forma

$A_{\theta}=\left(\begin{array}{cc}\cos(\theta)&-\sin(\theta)\\\sin(\theta)&\cos(\theta)\end{array}\right)$ .

Este elemento es en efecto una rotación con centro en $i$ y de ángulo $-2\theta$ . Naturalmente, con lo que sabemos hasta ahora, visualizar esto no es evidente. Se hace necesario un modelo hiperbólico en el cual la geometría sea mucho más precisa y clarificante (pero pagando ese precio, perdemos facilidad en algunos cálculos).

Sea $\mathbb{D}=\{z\in\mathbb{C}:|z|<1\}$ , entonces la función $f:\mathbb{H}\rightarrow\mathbb{D}$ , definida por

$f(z)=\frac{z-i}{z+i}$

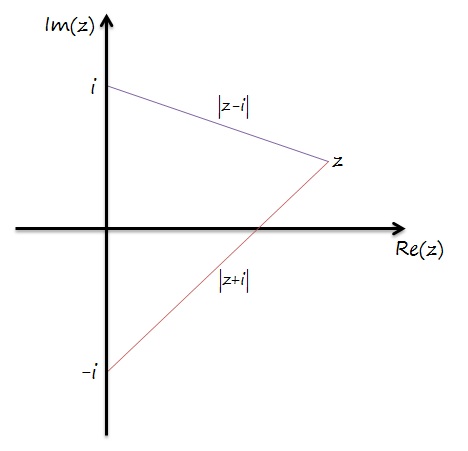
es una biyección. Debemos probar primero que nuestro recorrido es efectivamente el disco, para ello notamos que si $z\in\mathbb{H}$ entonces $|z-i|<|z+i|$ (ver figura), y por lo tanto $|f(z)|<1$ . Por otro lado, para $w\in\mathbb{D}$ se tiene que $\frac{i(w+1)}{1-w}$ es un elemento del plano hiperbólico, y es el único elemento tal que al componerla con $f$ me entrega nuevamente $w$ . Hemos encontrado una inversa continua.

Observación: Obtuvimos un homeomorfismo, que desde el punto de vista de variable compleja representa un biholomorfismo. En particular los ángulos se preservan.

A modo de observación, podemos definir una métrica en $\mathbb{D}$ dada por $|ds|=\frac{|g'(z)||dz|}{Im(g(z))}$ , la cual de manera intuitiva representa la métrica imagen vía $g=f^{-1}$ (las distancias entre dos puntos del disco son las distancias de las imagenes vía $g$ ). Un simple cálculo muestra que

$|ds|=\frac{2|dz|}{1-|z|^{2}}$ .

Ejercicio: Verificar que las geodésicas del disco con esta métrica son, o bien segmentos de circunferencias ortogonales al borde del disco unitario, o bien segmentos de rectas que pasan por el origen.

Observación: Por como definimos esta métrica, $f$ es una isometría.

Volviendo a lo que nos interesa, queremos representar en el plano hiperbólico las rotaciones. Como tenemos una aplicación conforme del plano en el disco, entonces podemos estudiar las rotaciones del disco (que son fáciles de representar) y trasladar nuestra información, vía nuestra aplicación, al semiplano:

Sabemos que $f(i)=0$ , por lo que una rotación con centro en «latex i» se traduce en el disco en una rotación con centro en el origen. Por otro lado, una rotación en ángulo $\theta$ en el disco es representado por $z\mapsto e^{i\theta}z$ . Matricialmente esta acción está dada por

$z\mapsto\left(\begin{array}{cc}e^{\theta/2}&{0}\\{0}&e^{-\theta/2}\end{array}\right)\cdot z$

por lo que, escribiendo $z\mapsto f(z)$ de la forma

$z\mapsto \left(\begin{array}{cc}{1}&{-i}\\{1}&{i}\end{array}\right)\cdot z$

nos queda, denotando $R_{\theta}$ la rotación en ángulo $\theta$ con centro en $i$ del plano hiperbolico,

$R_{\theta}=\frac{1}{2i}\left(\begin{array}{cc}{i}&{i}\\{-1}&{1}\end{array}\right)\left(\begin{array}{cc}e^{\theta/2}&{0}\\{0}&e^{-\theta/2}\end{array}\right)\left(\begin{array}{cc}{1}&{-i}\\{1}&{i}\end{array}\right)$

o escrito en forma reducida

$R_{\theta}=\left(\begin{array}{cc}\cos{\theta/2}&\sin{\theta/2}\\-\sin{\theta/2}&\cos{\theta/2}\end{array}\right)$ .

Notar que esto muestra nuestra primera afirmación. De acuerdo a la matriz escrita al comienzo, $A(\theta)$ es exactamente una rotación en ángulo $-2\theta$ .

Resumiendo, en los últimos dos post hemos escrito tres tipos de matrices, de acuerdo a su comportamiento dinámico, y dos de acuerdo a su acción geométrica en el plano hiperbólico. Éstas son

$R_{\theta}=\left(\begin{array}{cc}\cos{\theta/2}&\sin{\theta/2}\\-\sin{\theta/2}&\cos{\theta/2}\end{array}\right)$

$T_{d}=\left(\begin{array}{cc}e^{d/2}&{0}\\{0}&e^{-d/2}\end{array}\right)$

La primera representando una rotación en ángulo $\theta$ y centro $i$ (el cual es fijo), y la segunda representando un elemento hiperbólico con dos puntos fijos $0,\infty$ y con distancia de desplazamiento $d$ .

Si aplicamos entonces la matriz $R_{\pi/2}$ a $T_{d}$ nos queda (como vimos en el post anterior) un elemento hiperbólico con punto repulsor $-1$ y atractor $1$ . A saber, el elemento

$\left(\begin{array}{cc}\cosh{d/2}&\sinh{d/2}\\\sinh{d/2}&\cosh{d/2}\end{array}\right)$

Representación Adjunta

Una herramienta útil en el estudio algebraico de las acciones dada por el grupo $PSL(2,\mathbb{R})$ está dada por la representación adjunta. Para introducirla debemos definir el grupo $sl(2,\mathbb{R})$ .

Definición: El grupo $sl(2,\mathbb{R})$ se define como el grupo (aditivo) de todas las matrices con traza nula.

Notar que $sl(2,\mathbb{R})$ tiene una estructura de espacio vectorial real. Ademas, el grupo $SL(2,\mathbb{R})$ actúa en $sl(2,\mathbb{R})$ por conjugación. En efecto, si

$A=\left(\begin{array}{cc}a&b\\c&d\end{array}\right)\in SL(2,\mathbb{R})$ y $X=\left(\begin{array}{cc}x&y\\z&-x\end{array}\right)\in sl(2,\mathbb{R})$

se tiene

$AXA^{-1}=\left(\begin{array}{cc}a&b\\c&d\end{array}\right)\left(\begin{array}{cc}x&y\\z&-x\end{array}\right)\left(\begin{array}{cc}d&-b\\-c&a\end{array}\right)$

$=\left(\begin{array}{cc}(ad+bc)x+bdz-acy&-b^{2}+a^{2}y-2abx\\d^{2}z-c^{2}y+2cdx&-(ad+bc)x-bdz+acy\end{array}\right)$

de donde es claro que $tr(AXA^{-1})=0$ (por lo que la acción está bien definida).

Implicitamente escribimos $X$ con cierta estructura que deja en evidencia una base (visto como espacio vectorial). Escogemos entonces una base para $sl(2,\mathbb{R})$ la dada por

$e_{1}=\left(\begin{array}{cc}{1}&{0}\\{0}&{-1}\end{array}\right)$ , $e_{2}=\left(\begin{array}{cc}{0}&{1}\\{1}&{0}\end{array}\right)$ y $e_{3}=\left(\begin{array}{cc}{0}&{1}\\{-1}&{0}\end{array}\right)$

Y por lo tanto, si definimos la aplicación adjunta de $A$ como $Ad(A):sl(2,\mathbb{R})\rightarrow sl(2,\mathbb{R})$ , en la base anterior se escribe matricialmente como

$Ad(A)=\left(\begin{array}{ccc}{ad+bc}&{bd-ac}&-ac-bd\\-ab+cd&\frac{1}{2}(a^{2}-b^{2}-c^{2}+d^{2})&\frac{1}{2}(a^{2}+b^{2}-c^{2}-d^{2})\\-ab-cd&\frac{1}{2}(a^{2}-b^{2}+c^{2}-d^{2})&\frac{1}{2}(a^{2}+b^{2}+c^{2}+d^{2})\end{array}\right)$

Y por lo tanto hemos definido una aplicación (o representación), llamada adjunta, de la forma $ad:SL(2,\mathbb{R})\rightarrow End(sl(2,\mathbb{R}))$ . Es posible verificar que $Ker(ad)=\pm Id$ .

Por último debemos recordar que estamos trabajando sobre un espacio vectorial, y para facilitar los calculos, es mejor trabajar con la adjunta de las matrices elementales que encontramos. Éstos son los tres casos principales

Si $A=\left(\begin{array}{cc}e^{d/2}&{0}\\{0}&e^{-d/2}\end{array}\right)$ , entonces $Ad(A)=\left(\begin{array}{ccc}{1}&{0}&{0}\\{0}&\cosh(d)&\sinh(d)\\{0}&\sinh(d)&\cosh(d)\end{array}\right)$
Si $A=\left(\begin{array}{cc}\cosh(d/2)&\sinh(d/2)\\\sinh(d/2)&\cosh(d/2)\end{array}\right)$ , entonces $Ad(A)=\left(\begin{array}{ccc}{\cosh(d)}&{0}&-\sinh(d)\\{0}&{1}&{0}\\{-\sinh(d)}&{0}&\cosh(d)\end{array}\right)$
Si $A=\left(\begin{array}{cc}\cos(\theta/2)&\sin(\theta/2)\\-\sin(\theta/2)&\cos(\theta/2)\end{array}\right)$ , entonces $Ad(A)=\left(\begin{array}{ccc}{\cos(\theta)}&{\sin(\theta)}&{0}\\{-\sin(\theta)}&{\cos(\theta)}&{0}\\{0}&{0}&{1}\end{array}\right)$ .