En este post se asumirá que el lector tiene un conocimiento en superficies de Riemann y topología algebraica.
Definición: Un grupo Fuchsiano es un subgrupo discreto de  .
.
Observación: Aquellos que conocen el Teorema de Uniformización, probablemente tengan en mente el siguiente resultado. Una superficie de Riemann compacta de género mayor o igual a 2 proviene del cuociente del disco unitario con un subgrupo de isometrías del disco. Este subgrupo es isomorfo al grupo fundamental, y por lo tanto, en vista del isomorfismo excepcional  , concluimos que dicho grupo de isometrías es un grupo fuchsiano (o isomorfo a uno).
, concluimos que dicho grupo de isometrías es un grupo fuchsiano (o isomorfo a uno).
Primero intentaremos caracterizar a los grupos Fuchsianos, una forma se basa en el lema siguiente. De aquí en adelante denotaremos 
Lema:  es Fuchsiano si y solamente si él actua discontinuamente (todas las órbitas discretas) en
es Fuchsiano si y solamente si él actua discontinuamente (todas las órbitas discretas) en  .
.
Demostración:
El grupo  actúa libre y transitivamente sobre el fibrado tangente unitario
actúa libre y transitivamente sobre el fibrado tangente unitario  (pensar en el espacio tangente de
(pensar en el espacio tangente de  considerando direcciones unitarias, si fija un punto y una dirección, debe ser la identidad). Luego
considerando direcciones unitarias, si fija un punto y una dirección, debe ser la identidad). Luego  es discreto, si y solamente si, la acción en el fibrado es discreto. Así, las órbitas son discretas en
es discreto, si y solamente si, la acción en el fibrado es discreto. Así, las órbitas son discretas en  si y solamente si lo son en
si y solamente si lo son en  .
.

Definición: Un polígono de  es un subconjunto cerrado, convexo, con borde geodésico por tramos. Un lado es un segmento geodésico maximal en el borde y un vértice (definicion temporal) es un punto del borde definido por ser la intersección de dos lados. El polígono se dice finito si tiene un número finito de lados.
es un subconjunto cerrado, convexo, con borde geodésico por tramos. Un lado es un segmento geodésico maximal en el borde y un vértice (definicion temporal) es un punto del borde definido por ser la intersección de dos lados. El polígono se dice finito si tiene un número finito de lados.
El objetivo de este post es enunciar (y dar una intuición antes de eso) el Teorema del Polígono de Dirichlet.
Definición: Un polígono  se dice fundamental para el grupo
se dice fundamental para el grupo  si las traslaciones de
si las traslaciones de 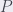 por el grupo
por el grupo  cubren
cubren  y las translaciones del interior del polígono son dos a dos disjuntas.
y las translaciones del interior del polígono son dos a dos disjuntas.
Definición: Un polígono de Dirichlet  asociado a
asociado a  y centrado en
y centrado en  es el conjunto
es el conjunto
 .
.
Con estas definiciones, es posible probar que para  un grupo Fuchsiano y
un grupo Fuchsiano y  de estabilizador trivial en
de estabilizador trivial en  , entonces el poligono de Dirichlet
, entonces el poligono de Dirichlet  es un polígono (segun nuestra primera definición). Mas aún, dicho polígono es fundamental.
es un polígono (segun nuestra primera definición). Mas aún, dicho polígono es fundamental.

Consideramos entonces un grupo Fuchsiano  y un polígono de Dirichlet
y un polígono de Dirichlet  centrado en un punto con estabilizador trivial. El objetivo de los siguientes parrafos es encontrar una representación del grupo.
centrado en un punto con estabilizador trivial. El objetivo de los siguientes parrafos es encontrar una representación del grupo.
Lema: Sea  . Entonces existe
. Entonces existe  tal que
tal que  pertenece también a
pertenece también a  . Además, un tal
. Además, un tal  es único si
es único si  no es un vértice.
no es un vértice.
Demostración:
Por la definición de polígono de Dirichlet,  si y solamente si existe
si y solamente si existe  tal que la distancia de
tal que la distancia de  a
a  (la orbita de
(la orbita de  ) es alcanzada por
) es alcanzada por  y
y  . Así, la distancia de
. Así, la distancia de  a
a  es igual (recordar que la acción es por isometrías) a la distancia entre
es igual (recordar que la acción es por isometrías) a la distancia entre  y
y  , y por tanto nuestro elemento buscado es
, y por tanto nuestro elemento buscado es  . Recíprocamente, si
. Recíprocamente, si  y
y  están en el borde del polígono, entonces
están en el borde del polígono, entonces  es equidistante de
es equidistante de  y
y  .
.
Si existiera un  tal que
tal que  está en la frontera del polígono, entonces
está en la frontera del polígono, entonces  y luego, si
y luego, si  entonces
entonces  esta en la intersección de los polígonos fundamentales
esta en la intersección de los polígonos fundamentales  . Como los polígonos cubren a
. Como los polígonos cubren a  se tiene que
se tiene que  debe ser un vértice.
debe ser un vértice.

Naturalmente, el lema anterior no nos especifica si uno podría tener que  . La igualdad puede ser alcanzada por los vértices, pero también por los puntos medios de los segmentos geodésicos (deben pensar que no puede ser otro punto del segmento pues debe haber una acción por isometría). Definimos entonces los vértices del polígono como los vértices ya definidos unidos a los puntos medios de los segmentos que satisfacen la igualdad anterior (es decir, tienen estabilizador no trivial). Con esta nueva definición, un punto en el borde que no es un vértice, debe tener por imagen (vía el único elemento del grupo descrito como antes) un punto del borde del polígono en un segmento geodésico que no es el mismo al cual pertenece. Si enumeramos los lados
. La igualdad puede ser alcanzada por los vértices, pero también por los puntos medios de los segmentos geodésicos (deben pensar que no puede ser otro punto del segmento pues debe haber una acción por isometría). Definimos entonces los vértices del polígono como los vértices ya definidos unidos a los puntos medios de los segmentos que satisfacen la igualdad anterior (es decir, tienen estabilizador no trivial). Con esta nueva definición, un punto en el borde que no es un vértice, debe tener por imagen (vía el único elemento del grupo descrito como antes) un punto del borde del polígono en un segmento geodésico que no es el mismo al cual pertenece. Si enumeramos los lados  , estos son aquellos tales que para cada
, estos son aquellos tales que para cada  existe un único
existe un único  del grupo, y un único
del grupo, y un único  tal que
tal que  envia
envia  en
en  (y este invierte la orientación dada por la la usual como borde de un conjunto convexo).
(y este invierte la orientación dada por la la usual como borde de un conjunto convexo).
Lo anterior nos dice que un polígono con cantidad finita de lados, debe tener cardinalidad de lados par. Además, por unicidad, es claro que  . Escribimos
. Escribimos  a tal involución.
a tal involución.
Definición: El par  se conoce como apareamiento de lados para el polígono
se conoce como apareamiento de lados para el polígono  .
.
Proposición: Suponiendo que 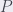 es finito, entonces
es finito, entonces  es generado por los
es generado por los  .
.
Demostración:
Sea  . Si
. Si  es uno de los
es uno de los  , entonces
, entonces  pertenece a una copia de
pertenece a una copia de 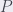 vecina a
vecina a 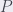 . Si no, consideremos un camino de
. Si no, consideremos un camino de  a
a  que evita vértices y es transversal a los lados (de todas las traslaciones de
que evita vértices y es transversal a los lados (de todas las traslaciones de 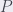 en caso que las intersecte). Consideramos la sucesion finita
en caso que las intersecte). Consideramos la sucesion finita  de lados tales que el camino los cruza. Cada uno de esos lados es la imagen de un unico lado
de lados tales que el camino los cruza. Cada uno de esos lados es la imagen de un unico lado  de
de 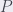 . De esta forma, el vecino de
. De esta forma, el vecino de 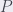 a lo largo de
a lo largo de  es por construccion la traslacion
es por construccion la traslacion  . No es dificil de ver que
. No es dificil de ver que  . Con esto se concluye que
. Con esto se concluye que  .
.
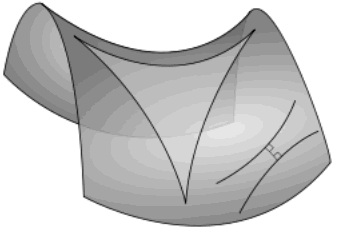
En la figura adjunta se muestra un diseño de lo que sucede (los cambios de notacion son evidentemente adecuables a nuestra escritura)


Por último, podemos definir una relación de equivalencia entre los vértices del polígono. Dos vértices se relacionan si existe un elemento del grupo que envía uno en otro. Llamamos ciclo elíptico a una clase de equivalencia. Además, un ciclo es determinado por una cantidad finita de vértices debido al cubrimiento de las traslaciones del polígono y la discretitud del grupo. Finalmente se define como ángulo de un ciclo a la suma de los ángulos del polígono en cada vértice del ciclo.
Definición: Denotamos  . Si escribimos
. Si escribimos  , entonces el ciclo de
, entonces el ciclo de  es
es  donde
donde  es el primer entero tal que
es el primer entero tal que  .
.
Proposición: El ángulo de un ciclo es de la forma  para
para  . En tal caso
. En tal caso  genera el estabilizador de
genera el estabilizador de  y es de orden
y es de orden  .
.
Demostración:
Por construcción  fija
fija  , luego es de orden finito (por ser discreto). Cualquier elemento
, luego es de orden finito (por ser discreto). Cualquier elemento  que fija
que fija  debe ser una rotación en ángulo el ángulo del ciclo. Es fácil ver que tal el elemento debe ser de la forma
debe ser una rotación en ángulo el ángulo del ciclo. Es fácil ver que tal el elemento debe ser de la forma  donde
donde  es un multiplo de
es un multiplo de  .
.

Si resumimos, partiendo de un grupo Fuchsiano y un polígono de Dirichlet asociado, encontramos un apareamiento de lados, una involución que describe el apareamiento. Cada vértice pertenece a un ciclo, con ángulo de ciclo dividiendo a  . Los elementos que relacionan los lados satisfacen
. Los elementos que relacionan los lados satisfacen  y
y  donde el ángulo de ciclo es
donde el ángulo de ciclo es  .
.
Con esto en mente, es natural preguntarse si existe algún tipo de recíproco. En efecto
Teorema (Polígono de Poincaré)
Sea 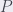 un polígono compacto de lados
un polígono compacto de lados  con un apareamiento
con un apareamiento  tal que el ángulo de cada ciclo divide a
tal que el ángulo de cada ciclo divide a  . Entonces el grupo
. Entonces el grupo  generado por los
generado por los  es Fuchsiano y de representación
es Fuchsiano y de representación
 .
.
Debemos hacer una observacion no menor. Este resultado es mucho mas general, para (por ejemplo) un polígono no compacto, el cual tiene vértices en la frontera del plano hiperbólico. Estos vértices se conocen como vértices en el infinito, y sus ciclos se llaman ciclos parabólicos (pues la isotropía en esos puntos son elementos parabólicos de  ). ¡Es un resultado precioso!.
). ¡Es un resultado precioso!.
Para concluir con este post, mostraremos una pequeña aplicación de estos resultados
Grupos Fuchsianos y Superficies de Riemann
Sea 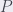 un polígono de
un polígono de  lados, de área finita, con un apareamiento
lados, de área finita, con un apareamiento  . Escribimos
. Escribimos  la cantidad de ciclos elípticos y
la cantidad de ciclos elípticos y  la cantidad de ciclos parabólicos.
la cantidad de ciclos parabólicos.
Proposición: Si 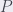 satisface las hipótesis del Teorema de Poincaré y
satisface las hipótesis del Teorema de Poincaré y  es el grupo generado por los
es el grupo generado por los  , entonces el cuociente de
, entonces el cuociente de  por
por  es una superficie de Riemann compacta de género
es una superficie de Riemann compacta de género

Demostración:
Las cartas para los puntos en las traslaciones del interior del polígono se definen por la identidad para una vecindad suficientemente pequeña. En los vértices elípticos se definen por  donde
donde  representa el ángulo del ciclo, y en los vértices en el infinito debemos ser mas sutiles. Después de conjugar, supongamos que el vértice es
representa el ángulo del ciclo, y en los vértices en el infinito debemos ser mas sutiles. Después de conjugar, supongamos que el vértice es  y que el elemento parabólico definido por el ciclo es
y que el elemento parabólico definido por el ciclo es  . Entonces la función
. Entonces la función  define una carta local. La compacidad proviene del cubrimiento finito definido por estas cartas (o también se puede pensar que estamos compactificando la superficie
define una carta local. La compacidad proviene del cubrimiento finito definido por estas cartas (o también se puede pensar que estamos compactificando la superficie  ) y el cálculo del género resulta de trazar triángulos desde el centro del polígono a los vértices (mirado todo en el plano hiperbólico) y luego cuocientamos y usamos la característica de Euler. Modulo la acción la triangulación nos queda con
) y el cálculo del género resulta de trazar triángulos desde el centro del polígono a los vértices (mirado todo en el plano hiperbólico) y luego cuocientamos y usamos la característica de Euler. Modulo la acción la triangulación nos queda con  triángulos,
triángulos,  vértices y
vértices y  aristas. Es decir,
aristas. Es decir,  .
.

Bibliografía:
[Sai2011] _____, Uniformisation des surfaces de Riemann, ENS Éditions, 2011.
;
de
son estables por la diferencial, es decir
para todo
,
.
,
,
son medibles. La propiedad de estabilidad por la diferencial implica que tales aplicaciones son también invariantes por
. En el caso particular de
medida ergódica, las aplicaciones son constantes
– casi todas partes.
son llamados Exponentes de Lyapunov y los espacios
son llamados Espacios Característicos.