Sobre subsucesiones

28 febrero, 2013 de nfalvarado

1.- Si una sucesión monótona tiene una subsucesión convergente, demuestre que la sucesión converge.

Solución: Probaremos que la sucesión está acotada, ya que si ésta es monótona y está acotada, converge.

Sea $(x_k)$ una sucesión monótona (supongamos creciente). En particular, tenemos una subsucesión creciente, y por enunciado, convergente.

Definimos la subsucesión $(x_{n_{k}})$ como { $x_{n_{1}}$ , $x_{n_{2}}$ , …, $x_{n_{k}}$ , … }= $X$ tal que $x_{n_{k}}\leq x_{n_{k+1}}$

Ahora, como sabemos que la subsucesión converge, ésta está acotada. Luego $x_{n_{k}}\rightarrow L$ cuando $k\rightarrow\infty$ , donde $L=\sup{X}.$ Entonces $x_{n_{k}}\leq L$ para todo $k\in N.$

Por otro lado, como $x_k$ es creciente, existe $f: \mathbb{N}\rightarrow \mathbb{N}$ tal que $f(k)=n_k$ con $f$ creciente, es decir que $k\leq n_k$ para todo $k$ en $\mathbb{N}$ , por lo tanto $x_k \leq x_{n_k}\leq L$ , luego $x_k\leq L$

Entonces, como $(x_k)$ está acotada y es monótona (creciente), converge.

La Proyección Estereográfica

27 febrero, 2013 de Felipe Riquelme

La proyección estereográfica representa una aplicación continua definida desde la esfera de Riemann hacia el plano (ya sea $\mathbb{R}^{2}$ o $\mathbb{C}$ ). Sus aplicaciones son numerosas, y van desde nociones topológicas (como la compactificación de un conjunto) hasta nociones de geometría diferencial o compleja.

Idea de la construcción: Como en la figura adjunta, trazaremos una recta desde el polo norte de la esfera unitaria hasta el plano complejo. Esta recta intersecta a la esfera en un punto distinto al polo, y además al plano. Esta identificación entre puntos de intersección es la biyección que buscamos establecer.

Sea entonces $N=(0,0,1)$ el polo norte, $p=(X,Y,Z)$ un punto en la esfera $\mathbb{S}^{2}$ y $(x,y)$ el punto del plano $\mathbb{R}^{2}$ determinado por la intersección de la recta que pasa por $N$ y $p$ con el plano. Si llamamos $L$ a dicha recta y si escribimos $(x,y,0)$ como el punto del plano inmerso en $\mathbb{R}^{3}$ , nos queda

$L=\{(0,0,1)+t((X,Y,Z)-(0,0,1)):t\in\mathbb{R}\}$

de modo que debemos encontrar $t$ tal que la tercera coordenada sea nula. Un punto típico de la recta $L$ tiene la forma $(tX,tY,t(Z-1)+1)$ , de donde se concluye que $t=\frac{1}{1-Z}$ es el parámetro buscado. Con esto, el punto del plano que representa la proyección es de la forma

$\pi_{N}(p)=(\frac{X}{1-Z},\frac{Y}{1-Z})$

Notar que todo punto de $\mathbb{S}^{2}$ , salvo $N$ , satisface que su tercera coordenada es distinta de 1, por lo que $\pi_{N}(p)$ esta bien definida para todo $p\in\mathbb{S}^{2}\setminus\{N\}$ .

Hemos definido entonces una aplicación $\pi_{N}:\mathbb{S}^{2}\setminus\{N\}\rightarrow\mathbb{R}^{2}$ . Mostremos que es inyectiva, en efecto

$\pi_{N}(X,Y,Z)=\pi_{N}(U,V,W)\Leftrightarrow$ $\frac{X}{1-Z}=\frac{U}{1-W}$ y $\frac{Y}{1-Z}=\frac{V}{1-W}$

pero $X^{2}+Y^{2}+Z^{2}=1$ y $U^{2}+V^{2}+W^{2}=1$ , lo que implica

$\frac{1+Z}{1-Z}=\frac{1+W}{1-W}$

con lo que al desarrollar nos queda $Z=W$ lo que implica directamente $X=U$ y $Y=V$ .

Mostremos ahora que esta aplicación es sobreyectiva. En efecto, para un punto $(x,y)$ en el plano, lo consideramos como $(x,y,0)$ y escribimos la recta que lo une con $N$

$L'=\{(0,0,1)+s((x,y,0)-(0,0,1)):s\in\mathbb{R}\}$

de donde un punto de $L'$ es de la forma $(sx,sy,1-s)$ . Un tal punto pertenece a la esfera si y sólo si $(sx)^{2}+(sy)^{2}+(1-s)^{2}=1$ . Esto ocurre para $s=0$ (caso que no admitimos pues considerariamos el polo norte) o para $s=\frac{2}{x^{2}+y^{2}+1}$ , por lo que

$p=(X,Y,Z)=(\frac{2x}{x^{2}+y^{2}+1},\frac{2y}{x^{2}+y^{2}+1},\frac{x^{2}+y^{2}-1}{x^{2}+y^{2}+1})$ .

Mas aún, es claro que $\pi^{-1}_{N}:\mathbb{R}^{2}\rightarrow\mathbb{S}^{2}$ definida por

$\pi^{-1}_{N}(x,y)=(\frac{2x}{x^{2}+y^{2}+1},\frac{2y}{x^{2}+y^{2}+1},\frac{x^{2}+y^{2}-1}{x^{2}+y^{2}+1})$

es la inversa deseada.

Por último, debemos notar que sobre cada dominio, la función $\pi_{N}$ y su inversa son continuas. Por lo tanto la proyeccion estereográfica es un homeomorfismo.
Debemos además recalcar algo demasiado importante. El infinito (del plano) esta representado por el polo norte de la esfera de Riemann.

Proposición: La proyección estereográfica mapea círculos (de la superficie de la esfera) en círculos (generalizados) del plano.

Por círculos generalizados nos referimos a círculos del plano o rectas.

Demostración:

Estudiemos primero la imagen de un círculo de la esfera vía la proyección. Un tal círculo es la intersección de un plano de la forma $AX+BY+CZ+D=0$ con $\mathbb{S}^{2}$ . La imagen de los puntos $(X,Y,Z)$ que satisfacen esta ecuación son de la forma $(x,y)$ y deben satisfacer (de acuerdo a la fórmula de la preimagen de la proyección)

$A\frac{2x}{x^{2}+y^{2}+1}+B\frac{2y}{x^{2}+y^{2}+1}+C\frac{x^{2}+y^{2}-1}{x^{2}+y^{2}+1}+D=0$

lo cual reescribimos como

$(C+D)(x^{2}+y^{2})+2Ax+2By-(C-D)=0$ ( $\star$ )

Notemos que hay dos posibilidades, si $C=-D$ entonces ( $\star$ ) es de la forma $Ax+By=C$ la cual representa ciertamente una recta en el plano. En este caso, la ecuación del plano original se transforma en $AX+BY+C(Z-1)=0$ , y por lo tanto el plano pasa por el polo norte. Entonces

Círculos esféricos que contienen al polo norte son mapeados en rectas del plano $\mathbb{R}^{2}$

En cualquier otro caso, la ecuación ( $\star$ ) representa una circunferencia del plano.

Círculos esféricos que no continen al polo norte son mapeados en círculos del plano $\mathbb{R}^{2}$

Y como la proyección es una biyección, si el plano tiene intersección no vacía con la esfera, entonces siempre obtendremos un círculo generalizado en el plano euclideano siendo la imagen de tal intersección no vacía.

Solo queda mostrar el recíproco, es decir, que todo círculo generalizado del plano euclideano es la imagen de una circunferencia en la esfera. Para esto, consideremos dos casos, el primero cuando tenemos una circunferencia del plano de la forma

$x^{2}+y^{2}+ax+by+c=0$

Definimos entonces $A,B,C,D$ tales que $2A=a$ , $2B=b$ , $C+D=1$ y $D-C=c$ . Es fácil comprobar que el plano $AX+BY+CZ+D=0$ intersecta a la esfera y tal intersección tiene por imagen todo punto que satisface la ecuacion

$x^{2}+y^{2}+ax+by+c=0$ .

En el caso en que contamos con una recta del plano de la forma $ax+by+c=0$ es suficiente considerar $2A=a$ , $2B=b$ , $C=D=\frac{-c}{2}$ . Esto concluye la demostración.

$\blacksquare$

Observaciones: Un ejercicio interesante es estudiar la imagen de circunferencias en la esfera por medio de la proyección estereográfica al aplicar isometrías en la esfera. Por ejemplo, si rotamos la esfera manteniendo el eje $Z$ fijo, entonces solo estamos considerando en el plano una rotación. Pero basta rotar la esfera de cualquier otra forma de modo que algunas rectas pasen a ser círculos y algunos círculos pasen a ser rectas. ¿Qué sucede si aplicamos otro tipo de isometrías, como las reflexiones?

Para concluir, sería super útil que ustedes comprobaran lo siguiente, si aplicamos la proyección estereográfica (bajo las mismas ideas) desde el polo sur (es decir, el punto $S=(0,0,-1)$ ) entonces obtenemos un homeomorfismo

$\pi_{S}:\mathbb{S}^{2}\setminus\{S\}\rightarrow\mathbb{R}^{2}$ , $(X,Y,Z)\mapsto(\frac{X}{1+Z},\frac{Y}{1+Z})$

$\pi^{-1}_{S}:\mathbb{R}^{2}\rightarrow\mathbb{S}^{2}\setminus\{S\}$ , $(x,y)\mapsto(\frac{2x}{x^{2}+y^{2}+1},\frac{2y}{x^{2}+y^{2}+1},\frac{1-x^{2}-y^{2}}{x^{2}+y^{2}+1})$

y finalmente podemos considerar la aplicación (muy útil en los primeros ejemplos de variedades complejas)

$\pi_{S}\circ\pi^{-1}_{N}:\mathbb{R}^{2}\setminus\{(0,0)\}\rightarrow\mathbb{R}^{2}\setminus\{(0,0)\}$

$(x,y)\mapsto(\frac{x}{x^{2}+y{2}},\frac{-y}{x^{2}+y^{2}})$

Para tener una imagen mas clara, les dejamos este link de una parte del documental Dimensions

Nociones Básicas en Geometría Hiperbólica (Parte I)

21 febrero, 2013 de Felipe Riquelme

I. Historia

Durante gran parte de nuestros estudios (enseñanza básica y media en general) nos enseñan numerosos teoremas relacionados con la geometría; el Teorema de Pitágoras, Teorema de Thales, entre otros; pero esa geometría siempre lleva un mismo nombre, hablamos de la geometría Euclideana. Y la razón es simple, es la primera, y en muchos casos, única geometría con la que podemos lidiar desde el momento en que nacemos hasta que morimos. Sin embargo, a lo largo de los años, muchos matemáticos han trabajado sobre diversos modelos de geometría, ya sea la hiperbólica, la esférica o la proyectiva. En estos textos nos centraremos principalmente en el estudio del primero de ellos, la geometría Hiperbólica.

¿De dónde proviene la necesidad de crear una nueva geometría?

Probablemente la respuesta más concreta y certera es la curiosidad del matemático. Euclídes postuló 5 leyes sobre la geometría Euclideana, estos son

Una recta puede trazarse desde un punto cualquiera hasta otro.
Una recta finita (o segmento de recta) puede prolongarse continuamente y hacerse una recta infinita.
Una circunferencia puede describirse con un centro y una distancia.
Todos los ángulos rectos son iguales entre sí.
Por un punto exterior a una rectam es posible trazar una única recta paralela a dicha recta.

Entonces lo natural sería preguntarse si existen modelos de geometría que no satisfagan algunas de estas leyes.
Por mucho tiempo se creyó que las cuatro primeras leyes implicaban el quinto postulado, pero eventualmente se cambió la manera de abordar el problema. Los matemáticos empezaron a trabajar en la negación de este resultado. ¡Y lo lograron!, Nikolai Lobachevsky (matemático del siglo XIX) encontró un modelo geométrico consistente que satisface las primeras cuatro leyes y no la quinta. Fue el nacimiento de la Geometría Hiperbólica.

II. Preliminares

Para comenzar a entender la geometría hiperbólica y las propiedades de ésta, debemos imperativamente entender lo que es una métrica Riemanniana.
En abstracto, si considero un subconjunto abierto $X\subset\mathbb{R}^{n}$ del espacio euclideano, una métrica Riemanniana es una forma bilineal definida positiva de la forma $TX\times TX\rightarrow\mathbb{R}$ , donde $TX$ representa el espacio tangente de $X$ .

Naturalmente la anterior definición puede sonar algo intimidante para los que no tienen conocimientos muy profundos en matemática, pero a modo de ejemplo consideremos un punto $p\in X$ y una curva $\gamma:(-a,a)\rightarrow X$ continua, diferenciable en una vecindad del origen (estamos suponiendo $a>0$ arbitrario), tal que $\gamma(0)=p$ . Entonces $\gamma'(0)$ es ciertamente un «vector» que vive en $\mathbb{R}^{n}$ . Decimos en este sentido que $\gamma'(0)$ es un elemento de $T_{p}(X)$ , el espacio tangente a $X$ en $p$ . Si consideramos una curva $\delta$ de mismas características (salvo por su dominio que denotamos $(-b,b)$ para $b>0$ ), entonces $\delta'(0)\in T_{p}X$ y $c(t)=\frac{1}{2}(\gamma(2t)+\delta(2t))$ definida para $t\in(-\min(\frac{a}{2},\frac{b}{2}),\min(\frac{a}{2},\frac{b}{2}))$ satisface $c(0)=p$ y $c'(0)=\gamma'(0)+\delta'(0)$ . Naturalmente, si multiplico $\gamma$ por un escalar, entonces su vector tangente será ponderado por ese mismo escalar.

Todo el parrafo anterior nos dice que hay una cierta estructura de espacio vectorial sobre nuestro espacio tangente en $p$ . Pero claramente no hemos definido formalmente el espacio tangente, sin embargo estamos a un pequeño paso de hacerlo.

Hay muchas curvas que en el origen valen $p$ , y cuyo vector tangente en el origen es el mismo. Naturalmente no queremos hacer distinciones en este caso. Decimos entonces que dos curvas $\gamma$ y $\delta$ , como antes, están relacionadas $\gamma$ ~ $\delta$ si $\gamma$ y $\delta$ están definidas en una vecindad del origen, en el cual son diferenciables, tales que en el origen valen $p$ y su vector tangente en el origen es el mismo. No es difícil ver que esta es una relación de equivalencia.

Definimos entonces (de manera bastante abstracta)

$T_{p}X=\{[\gamma]\}$

donde, insistimos, $\gamma$ es de la forma que describimos anteriormente, y $[\gamma]$ representa la clase de equivalencia con la relación ~.

Observación: Esta es una manera bastante formal de ver el espacio tangente, pero si lo piensan profundamente (y naturalmente se deben convencer de ello) estamos considerando el espacio de todos los vectores tangente a $p$ (y no hacemos distinción de cual curva provienen metiendo a todas las de su tipo en un mismo saco).

Hemos probado (no muy formalmente, pero en esencia) que

Proposición: El espacio $T_{p}X$ es un espacio vectorial real. Más aún, su dimensión es la dimensión del espacio $X$ .

En lo anterior hay que tener cuidado, $X$ no es un espacio vectorial necesariamente, su dimensión se refiere al hecho de que es un abierto de $\mathbb{R}^{n}$ , por lo que su dimensión es $n$ .

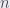Definición: El Fibrado Tangente, $TX$ es el conjunto $TX=\{(p,v):p\in X,v\in T_{p}X\}$ . Denotamos $\pi:TX\rightarrow X$ la proyección natural.

Teniendo esto claro, podemos ver una métrica Riemanniana $g$ como una forma bilineal definida positiva tal que en cada punto $p\in X$ , se tiene un producto interno (dada por la forma bilineal) sobre el espacio tangente a $X$ en $p$ . Es decir, al tener producto interno, obtenemos una noción clara de distancia.

Ejemplo: Una métrica Riemanniana sobre $\mathbb{R}^{2}$ es la estandar, la cual es de la forma $g=<X,Y>=X_{1}Y_{1}+X_{2}Y_{2}$ , donde $X=(X_{1},X_{2})$ y $Y=(Y_{1},Y_{2})$ son elementos del fibrado tangente. Sobre el tangente podemos definir una norma (la cual inducirá la métrica), $\|X\|^{2}=<X,X>$ . Más precisamente, si $\gamma:[-1,1]\rightarrow\mathbb{R}^{2}$ para $\gamma=(x(t),y(t))$ , entonces $\|\gamma'(t)\|^{2}=x'(t)^{2}+y'(t)^{2}$ .

Ahora que conocemos como es la métrica en el espacio tangente, podemos definir una distancia en $\mathbb{R}^{2}$ . La distancia entre dos puntos en el plano es el ínfimo de los largos de curvas que unen ambos puntos. Más precisamente, el largo de curva es

$L(\gamma)=\int_{t}\|\gamma'(t)\|dt$

con

$d(p,q)=\inf_{\gamma\textmd{ que unen }p,q }L(\gamma)$

Un simple cálculo muestra que bajo la métrica Riemanniana estandar sobre el espacio euclideo, se obtiene precisamente la métrica estandar (visto como espacio métrico).

Observaciones: Hay muchas cosas por hacer, ¿existen siempre curvas que minimizan distancias?, ¿por qué puedo pasar de una métrica definida a nivel local a algo a nivel global?. Pues bien, no es el objetivo de este post responder específicamente a cada pregunta, pero hay que confiar en lo que aquí se dice: tanto en la geometría Euclideana como en la Hiperbólica, estas preguntas (y muchas más que son naturales) tienen solución, y una buena respuesta, cuando nos reducimos a subconjuntos compactos de los espacios sobre los que se trabaja.

Un problema clásico

17 febrero, 2013 de Felipe Riquelme

Consideremos un cuadrado de lado 1. Sobre una de sus esquinas dibujamos un cuadrado de lado $\frac{1}{2}$ ; sobre el borde exterior de este nuevo cuadrado dibujamos en una de sus esquinas un cuadrado de lado $\frac{1}{4}$ , y así de manera recursiva… sobre el borde exterior del cuadrado n-ésimo, en una de sus esquinas, dibujamos un cuadrado de lado $\frac{1}{2^{n+1}}$ . Podemos hacer esto de manera ordenada como en la siguiente figura. La pregunta es… ¿cuál es la suma total de las áreas de los cuadrados así formados?

Naturalmente estamos sumando una cantidad infinita de cuadrados, por lo tanto, a priori, la suma de las áreas no tiene porque ser finita. Sin embargo, podemos utilizar el siguiente resultado

Proposición: Sea $\{a_{n}\}_{n>0}$ una sucesión de números reales, no decreciente y acotada superiormente. Entonces el límite $\lim_{n\rightarrow\infty}a_{n}$ existe (y es finito).

Demostración:

Sea $A=\{a_{n}\}_{n>0}$ visto como subconjunto de los numeros reales. El hecho de que la sucesión esté acotada superiormente implica que el conjunto $A$ tiene supremo; llamemoslo $L$ . Debemos mostrar que $L$ es el límite de la sucesión.

En efecto, si consideramos $\varepsilon>0$ , entonces $L-\varepsilon$ no es cota superior del conjunto, pues de serlo él sería menor que la menor cota superior del conjunto $A$ , contradiciendo que $L$ es supremo. Por lo tanto, existe un elemento $a_{N}$ de la sucesión para el cual se tiene $L-\varepsilon<a_{N}\leq L$ . Por otro lado la sucesión es no decreciente, por lo que para cada natural $n\geq N$ se tiene $a_{N}\geq a_{n}$ . Así mismo, como $A$ está acotado superiormente por el supremo, se satisface $a_{n}\leq L$ (en particular) para cada $n\geq N$ . Hemos mostrado entonces que

$L-\varepsilon<a_{n}\leq L$ para cada $n\geq N$ .

o equivalentemente

$|L-a_{n}|<\varepsilon$ para cada $n\geq N$ ,

la cual es precisamente la definición del límite.

$\blacksquare$

Notar entonces que en nuestro problema, podemos escribir $a_{n}$ como la suma de las áreas de los primeros $n$ cuadrados. Naturalmente, cada vez sumamos mas área, por lo que esta sucesión es no decreciente. Por último, es claro que la suma total es menor al area del cuadrado mayor, la cual es uno, por lo que $a_{n}$ está acotada por dicha área. Con esto, y gracias a nuestra reciente demostración, hemos probado que sumar las infinitas areas nos da un valor finito.

En la practica sin embargo, este problema es bastante mas fácil si lo abordamos directamente con cálculos numéricos. En efecto, el área de cada cuadrado es $\frac{1}{4^{i}}$ , por lo que la suma de las áreas de los primeros $i$ cuadrados nos queda

$\sum_{i=1}^{n}\frac{1}{4^{i}}$

y si llamamos $a_{n}$ a tal suma, como antes, obtenemos

$\frac{1}{4}a_{n}=\frac{1}{4}\sum_{i=1}^{n}\frac{1}{4^{i}}=\sum_{i=2}^{n+1}\frac{1}{4^{i}}$

por lo que

$\frac{3}{4}a_{n}=a_{n}-\dfrac{1}{4}a_{n}=\sum_{i=1}^{n}\frac{1}{4^{i}}-\sum_{i=2}^{n+1}\frac{1}{4^{i}}=\frac{1}{4}-\frac{1}{4^{n+1}}$

de donde se concluye que

$a_{n}=\frac{4}{3}(\frac{1}{4}-\frac{1}{4^{n+1}})$

con lo que cuando $n$ tiende a infinito, nos queda $L=\frac{1}{3}$ .

Hemos concluido entonces que el área azul en nustra figura es de $\frac{1}{3}$ . Quizás en la figura siguiente queda un poco mas graficado este resultado.

Conexidad

11 febrero, 2013 de Felipe Riquelme

La conexidad es una propiedad topológica de los conjuntos, es decir, su definición depende exclusivamente de los subconjuntos abiertos del espacio base. Recordemos que sobre el espacio euclideano n-dimensional se tienen abiertos «base», estas son las bolas (ya estudiadas bastante en este blog) que son de la forma

$B(x,r)=\{y\in\mathbb{R}^{n}:\|y-x\|<r\}$

donde $x\in\mathbb{R}^{n}$ y $r>0$ es un real positivo. Hemos visto que un conjunto abierto del espacio euclideano se caracteriza por la propiedad de que en cada punto existe una bola centrada en dicho punto, totalmente contenida en el conjunto.

Ahora veamos la definición de conexidad

Definición: Un conjunto $X\subset\mathbb{R}^{n}$ se dice conexo si no existen abiertos $A,B\subset\mathbb{R}^{n}$ disjuntos tal que $X\subset(A\cup B)$ , $X\cap A\neq\emptyset$ y $X\cap B\neq\emptyset$ .

En palabras simples, un conjunto conexo es aquel que no se puede separar por abiertos.

Ejemplos:

$\mathbb{R}^{n}$ es conexo. En efecto, supongamos que no es conexo, luego existen abiertos $A,B$ disjuntos, no vacíos, que satisfacen $\mathbb{R}^{n}=A\cup B$ . Al ser cada uno no vacío se tiene que existe $a\in A$ y $b\in B$ , de donde podemos considerar la curva que los une dada por $\gamma:[0,1]\rightarrow\mathbb{R}^{n}$ , definida por $\gamma(t)=bt+(1-t)a$ . Sea entonces $s\in[0,1]$ tal que $s=\sup\{t\in[0,1]:\gamma(t)\in A\}$ . La pregunta es… ¿ $\gamma(s)\in A$ o $\gamma(s)\in B$ ? Si estuviera en $A$ , entonces como $A$ es abierto se tiene que existe una bola en torno a $\gamma(s)$ , $B(\gamma(s),r)$ , totalmente contenida en $A$ , lo que implica (por continuidad de la curva), que existen valores de $t$ , arbitrariamente cerca (y mayores) de $s$ tal que $\gamma(t)\in A$ , lo que contradice que $s$ es el supremo escogido. De manera análoga podemos mostrar que $\gamma(s)$ no puede estar en $B$ . Esto es una contradicción, y por lo tanto $\mathbb{R}^{n}$ es conexo.
Un intervalo de la forma $(a,b)$ es conexo, la demostración es análoga a la anterior.
Otro ejemplo, algo trivial, es considerar $X=\{0,1\}$ con la topología discreta, es decir, los abiertos de $X$ son $\emptyset,\{0\},\{1\},X$ . En tal caso $X$ no es conexo pues puedo escribirlo como la unión de los abiertos no vacíos y disjuntos $\{0\},\{1\}$ .

De inmediato podemos encontrar una caracterización bonita e interesante de los conjuntos conexos.

Proposición: Sea $X\subset\mathbb{R}^{n}$ un subconjunto abierto del espacio euclideano. Entonces $X$ es conexo si, y solamente si, no existe función continua $f:X\rightarrow\{0,1\}$ sobreyectiva.

Observación: Aquí dotamos a $\{0,1\}$ de la topología discreta.

Demostración:

Si $X$ no es conexo, entonces podemos encontrar conjuntos abiertos $A,B$ disjuntos, tales que $A\cap X\neq\emptyset$ , $B\cap X\neq\emptyset$ y $X=A\cup B$ . Definimos entonces la función $latex f:X\rightarrow\{0,1\}$ por $f(x)=0$ para $x\in(A\cap X)$ y $f(x)=1$ para $x\in(B\cap X)$ . Ya que $A$ y $B$ son disjuntos, no hay problemas con la definición de $f$ , la función es sobreyectiva pues tanto $A\cap X$ como $B\cap X$ son no vacíos, y la continuidad proviene del hecho de que la preimagen de abiertos es abierto (ver post), en efecto, $f^{-1}(\{0\})=X\cap A$ , el cual es abierto, y $f^{-1}(\{1\})=X\cap B$ el cual también es abierto.

Por otro lado si existiese una función $f:X\rightarrow\{0,1\}$ sobreyectiva y continua, entonces podemos escribir $X=f^{-1}(\{0\})\cup f^{-1}(\{1\})$ , es decir, como unión de abiertos disjuntos no vacíos. Lo que implica que $X$ no es conexo.

Naturalmente, estas dos implicancias son los contrarecíprocos de las que debemos mostrar. Esto concluye la demostración.

$\blacksquare$

Observación: En la última proposición escogimos $X$ abierto sólo de manera conveniente. Hay una forma de generalizar esto, resultando super natural cuando hablamos de topología de subespacios, la cual evitamos en esta ocasión para no enredar la idea básica que queremos exponer.

Continuidad

10 febrero, 2013 de Felipe Riquelme

En este post nos centraremos en una caracterización determinante sobre las funciones continuas. Naturalmente, partiremos con la definición de una función continua definida sobre un subconjunto del espacio euclideano n-dimensional, y luego generalizaremos a un espacio métrico de manera natural.

Recordemos entonces la definición de continuidad

Definición: Una función $f:U\subset\mathbb{R}^{n}\rightarrow\mathbb{R}^{m}$ definida en un abierto $U$ de $\mathbb{R}^{n}$ es continua en un punto $x_{0}\in U$ , si y sólo si para todo $\varepsilon>0$ existe $\delta>0$ tal que

$\|x-x_{0}\|<\delta$ $\Rightarrow$ $\|f(x)-f(x_{0})\|<\varepsilon$ .

Una tal función se dice continua (sobre su dominio) si es continua en todo punto de su dominio.

Observaciones: En la definición anterior escribimos de manera idéntica $\|\cdot\|$ para referirnos a la norma euclideana sobre $\mathbb{R}^{n}$ y sobre $\mathbb{R}^{m}$ , naturalmente hacemos esto por simplicidad de notación.

Proposición: Una función $f:U\subset\mathbb{R}^{n}\rightarrow\mathbb{R}^{m}$ es continua si y sólo si para todo abierto $V\subset\mathbb{R}^{m}$ , el conjunto $f^{-1}(V)\subset\mathbb{R}^{n}$ es abierto. En este caso definimos $f^{-1}(V)$ como

$f^{-1}(V)=\{x\in U:f(x)\in V\}$ .

Observación: ¡Cuidado!, en ningún caso estamos suponiendo que la función sea invertible.

Demostración:

Supongamos que nuestra función es continua (en el sentido de la definición propuesta), y consideremos un abierto $V\subset\mathbb{R}^{m}$ . Si $f^{-1}(V)=\emptyset$ , entonces $f^{-1}(V)$ es abierto por definición. Si no, entonces para cada $x_{0}\in U\cap f^{-1}(V)$ definimos $y_{0}=f(x_{0})\in V$ . Como $V$ es abierto, existe una bola en torno a $y_{0}$ totalmente contenida en $V$ ; i.e. existe $\varepsilon_{0}>0$ tal que $B(y_{0},\varepsilon_{0})\subset V$ . Por definición de continuidad, dado tal $\varepsilon_{0}$ existe $\delta_{0}>0$ tal que

$\|x-x_{0}\|<\delta_{0}$ $\Rightarrow$ $\|f(x)-f(x_{0})\|<\varepsilon_{0}$ .

Pero debemos notar que $\|x-x_{0}\|<\delta_{0}$ es equivalente a decir $x\in B(x_{0},\delta_{0})$ , y por otro lado, $\|f(x)-f(x_{0})\|<\varepsilon_{0}$ es equivalente a decir $f(x)\in B(y_{0},\varepsilon_{0})$ . Por lo tanto de la definición de continuidad en el punto $x_{0}$ , se concluye que

$x\in B(x_{0},\delta_{0})$ $\Rightarrow$ $f(x)\in B(y_{0},\varepsilon_{0})$ .

Pero $B(y_{0},\varepsilon_{0})$ $\subset V$ , por lo que si $x\in B(x_{0},\delta_{0})$ entonces $f(x)\in V$ , de donde se concluye que

$f(B(x_{0},\delta_{0}))\subset V$

o de manera equivalente

$B(x_{0},\delta_{0})\subset f^{-1}(V)$ .

Hemos mostrado que para cada punto en el conjunto $f^{-1}(V)$ existe una bola, en torno a tal punto, totalmente contenida en $f^{-1}(V)$ . Esto resulta ser exactamente que $f^{-1}(V)$ es un conjunto abierto en $\mathbb{R}^{n}$ .

Para el recíproco, supongamos que para cada abierto $V$ en $\mathbb{R}^{m}$ el conjunto $f^{-1}(V)$ es abierto en $\mathbb{R}^{n}$ . Consideremos un punto $x\in U$ y su imagen $f(x)\in V$ . Para un $\varepsilon>0$ arbitrario podemos considerar en particular $V=B(f(x),\varepsilon)$ , y luego su preimagen $f^{-1}(B(f(x),\varepsilon))$ es abierta en $\mathbb{R}^{n}$ . Luego en torno a $x\in$ $f^{-1}(B(f(x),\varepsilon))$ existe una bola de radio $\delta>0$ , $B(x,\delta)$ , tal que

$B(x,\delta)\subset f^{-1}(B(f(x),\varepsilon))$

o equivalentemente

$f(B(x,\delta))\subset B(f(x),\varepsilon)$ .

Y como vimos anteriormente, esto es equivalente a $\|x-x_{0}\|<\delta$ $\Rightarrow$ $\|f(x)-f(x_{0})\|<\varepsilon$ , lo que muestra la continuidad en $x$ , y luego, por arbitrariedad de $x\in U$ , se tiene la continuidad en todo $U$ .

$\blacksquare$

De inmediato se obtienen resultados importantes por esta equivalencia. Entre ellos

Dada una función continua como antes, la preimagen de conjuntos cerrados es cerrado. Basta usar el hecho de que el complemento de una preimagen es la preimagen del complemento; i.e. para cada $V\subset\mathbb{R}^{m}$ , $(f^{-1}(V))^{c}=f^{-1}(V^{c})$ .
En particular de lo anterior, la preimagen de un punto es un conjunto cerrado.

Por otra parte, podemos generalizar un poco más esta nocion para espacios métricos. Si el lector no esta familiarizado, puede encontrar un link de interés haciendo click en «Espacios métricos«.

Proposición: Sea $F:(X,d)\rightarrow (Y,\rho)$ una función continua entre dos espacios métricos. Entonces la preimagen de todo abierto en $Y$ es un abierto en $X$ . Mas aún, esta es una equivalencia.

La demostración de lo anterior es exactamente idéntica a la demostración aquí realizada para el caso particular donde $f:(\mathbb{R}^{n},d_{E})\rightarrow (\mathbb{R}^{m},d_{E})$ . En este caso, $d_{E}$ denota la distancia euclideana.

Un problema sobre convergencias

2 febrero, 2013 de Felipe Riquelme

Definición: Un conjunto $I\subset\mathbb{N}$ se dice de densidad cero si

$\lim_{n\rightarrow\infty}\dfrac{\sharp(I\cap\{0,...,n-1\})}{n}=0$ .

Si consideramos ahora una sucesión $\{a_{n}\}_{n\in\mathbb{N}}$ de números reales, acotada, nos podemos preguntar si existe un subconjunto $I\subset\mathbb{N}$ de densidad cero tal que el límite

$\lim_{n\not\in I}a_{n}$

existe.

En el caso particular cuando $\lim_{n\not\in I}a_{n}=0$ para algún conjunto $I$ se tiene una caracterización bastante interesante.

Proposición: Para $\{a_{n}\}_{n\in\mathbb{N}}$ como antes, las afirmaciones siguientes son equivalentes

$\lim_{n\rightarrow\infty}\frac{1}{n}\sum_{i=0}^{n-1}|a_{i}|=0$
Existe $I\subset\mathbb{N}$ de densidad cero tal que $\lim_{n\not\in I}a_{n}=0$ .

Notación: Denotamos $\delta(I)=\lim_{n\rightarrow\infty}\dfrac{\sharp(I\cap\{0,...,n-1\})}{n}$ , $\delta_{n}(I)=\dfrac{\sharp(I\cap\{0,...,n-1\})}{n}$ y $C(I,n)=\sharp(I\cap\{0,...,n-1\})$ .

Para mostrar que (1) implica (2), consideramos un entero $k\geq 1$ y el conjunto

$I_{k}=\{n\geq 0:|a_{n}|\geq\frac{1}{k}\}$ ,

entonces dicho conjunto es de densidad cero pues

$\frac{1}{n}\sum_{i=0}^{n-1}|a_{i}|\geq\frac{1}{n}\sum_{i=0,i\in I_{k}}^{n-1}|a_{i}|\geq\frac{1}{k}\delta_{n}(I_{k})$

y por lo tanto, como el término de la izquierda tiende a cero, el de la derecha también cuando $n$ tiende a infinito.

Hasta ahora tenemos lo siguiente, para cada $k\geq 0$ y para cada $\varepsilon>0$ existe $N(k,\varepsilon)\in\mathbb{N}$ tal que si $n>N(k,\varepsilon)$ entonces $\delta_{n}(I_{k})<\varepsilon$ . Por lo tanto, si escogemos $\varepsilon=\frac{1}{k}$ , podemos escoger un entero $N(k)>0$ tal que $\delta_{n}(I_{k})<\frac{1}{k}$ para $n>N(k)$ . Mas aún, podemos escoger los términos $N(k)$ de modo que sean estrictamente crecientes. Escribimos en tal caso $\{n_{k}=N(k)\}_{k}$ una sucesión estrictamente creciente de números naturales con la propiedad siguiente: Para todo $n>n_{k}$ se tiene

$\delta_{n}(I_{k})<\frac{1}{k}$ .

Escribimos $I=\bigcup_{k\geq 0}(I_{k+1}\cap\{n_{k},...,n_{k+1}-1\})$ . Entonces para cada $n\in\{n_{k},...,n_{k+1}-1\}$ se tiene

$I\cap\{0,...,n-1\}\subset I_{k+1}\cap\{0,...,n-1\}$

y luego al considerar la cardinalidad de tales conjuntos y dividir por $n$ , nos queda

$\delta_{n}(I)\leq\delta_{n}(I_{k+1})\leq\frac{1}{k+1}$

de donde, haciendo tender $k$ a infinito (y por lo tanto $n$ también), resulta que

$\lim_{n\rightarrow\infty}\delta_{n}(I)=0$ .

Finalmente si $n\geq n_{k}$ no pertenece a $I$ , entonces $n$ no pertenece a $I_{k+1}$ y por lo tanto $|a_{n}|<\frac{1}{k+1}$ , de donde se concluye que $\lim_{n\not\in I}a_{n}=0$ .

Para el recíproco ((2) implica (1)), consideramos $K>0$ una cota superior de $\{|a_{n}|\}_{n\geq 0}$ . Para cada $\varepsilon>0$ existe $N(\varepsilon)$ tal que si $n>N(\varepsilon)$ entonces $C(I,n)<\varepsilon n$ y además $|a_{n}|<\varepsilon$ si $n\not\in I$ . Se deduce entonces que para cada $n>\max\{N(\varepsilon),\frac{KN(\varepsilon)}{\varepsilon}\}$

$\frac{1}{n}\sum_{i=0}^{n-1}|a_{i}|=\frac{1}{n}[\sum_{i\in I}^{n-1}|a_{i}|+\sum_{i<N(\varepsilon),i\not\in I}^{n-1}|a_{i}|+\sum_{N(\varepsilon)\leq i<n,i\not\in I}^{n-1}|a_{i}|]$

$\leq\frac{KC(I,n)}{n}+\frac{KN(\varepsilon)}{n}+\varepsilon\leq(K+2)\varepsilon$

lo que concluye la demostración.

Nociones Basicas

2 febrero, 2013 de nfalvarado

1) Supongamos que los vectores $x_1, x_2, x_3, ... x_n$ generan un espacio vectorial $X$ , y los vectores $y_1, y_2, y_3, ... y_j$ son linealmente independientes en $X$ . Entonces $j \leq n$ .

Desde que $x_1, x_2, x_3, ... x_n$ generan a $X$ , todo vector en $X$ puede ser escrito como una combinación lineal de $x_1, x_2, x_3, ... x_n$ .

En particular, $y_1= k_1x_1+ k_2x_2+ k_3x_3+ ...+ k_nx_n$ , con $k_i\in \mathbb{R}$ , e $i=1,...,n$ .

Por otra parte, como los vectores $y_1, y_2, y_3, ... y_j$ son l.i. (linealmente independientes) tenemos que $y_1\neq 0$ , entonces no todos los $k$ son iguales a $0$ . Vale decir $k_i\neq 0$ , para algún $i=1,...,n$ .

Luego, $x_i$ puede ser escrito como una combinación lineal de $y_1$ y los restantes $x_s$ (el resto de los vectores sin considerar el i-ésimo). Por lo tanto, el conjunto formado por los vectores $x$ , con $x_i$ reemplazado por $y_1$ genera a $X$ .

Ahora, si $j \geq n$ repetimos este paso $n-1$ veces más y concluimos que $y_1, y_2, y_3, ... y_n$ generan a $X$ .

Si $j>n$ estariamos en una contradicción respecto a la independencia lineal de los vectores $y$ , puesto que $y_{n+1}$ sería combinación lineal de $y_1, y_2, y_3, ... y_n$ .

Por lo tanto concluimos que $j \leq n$

2) Todas las bases de un espacio vectorial $X$ finito dimensional contienen el mismo número de vectores.

Recordemos que una base es un conjunto finito de vectores que genera a un espacio vectorial $X$ y estos son linealmente independientes.

Consideremos dos bases de $X$ , $x_1, x_2, x_3, ... x_n$ e $y_1, y_2, y_3, ... y_m$ . Entonces por la demostración anterior tenemos que $n\leq m$ y $m\leq n$ . Luego concluimos que $n=m$ .